3.2.5. Inversion Input File

Both the forward and inverse problems are solved using the e3d_v2.exe executable program. In both cases, the lines of the input file are the same. However in the case of forward modeling, some lines in the input file are not used by the code and can be given any value. The lines of input file are as follows:

Line #	Parameter	Description
1	Inversion Mesh	path to inversion mesh file
2	Observations File	path to observations file
3	Transmitters File	path to transmitters file
4	Receivers File	path to receivers file
5	Frequencies File	path to frequencies file
6	Initial/FWD Model	initial model/forward model
7	Reference Model	reference model
8	Susceptibility Model	background susceptibility model
9	Active Topography Cells	topography
10	Active Model Cells	active model cells
11	Cell Weights	additional cell weights
12	Face Weights	additional face weights
13	Norm Sparseness	set parameters to recover smooth, sparse or blocky models
14	beta_max beta_min beta_factor	cooling schedule for beta parameter
15	alpha_s alpha_x alpha_y alpha_z	weighting constants for smallness and smoothness constraints
16	Chi Factor	stopping criteria for inversion
17	iter_per_beta nBetas	set the number of Gauss-Newton iteration for each beta value
18	tol_ipcg max_iter_ipcg	set the tolerance and number of iterations for Gauss-Newton solve
19	Reference Model Update	reference model
20	Hard Constraints	use SMOOTH_MOD or SMOOTH_MOD_DIFF
21	Bounds	upper and lower bounds for recovered model
22	Field Options	model total field or secondary field
23	Memory Options	options for storing factorizations of forward system (RAM vs disk)

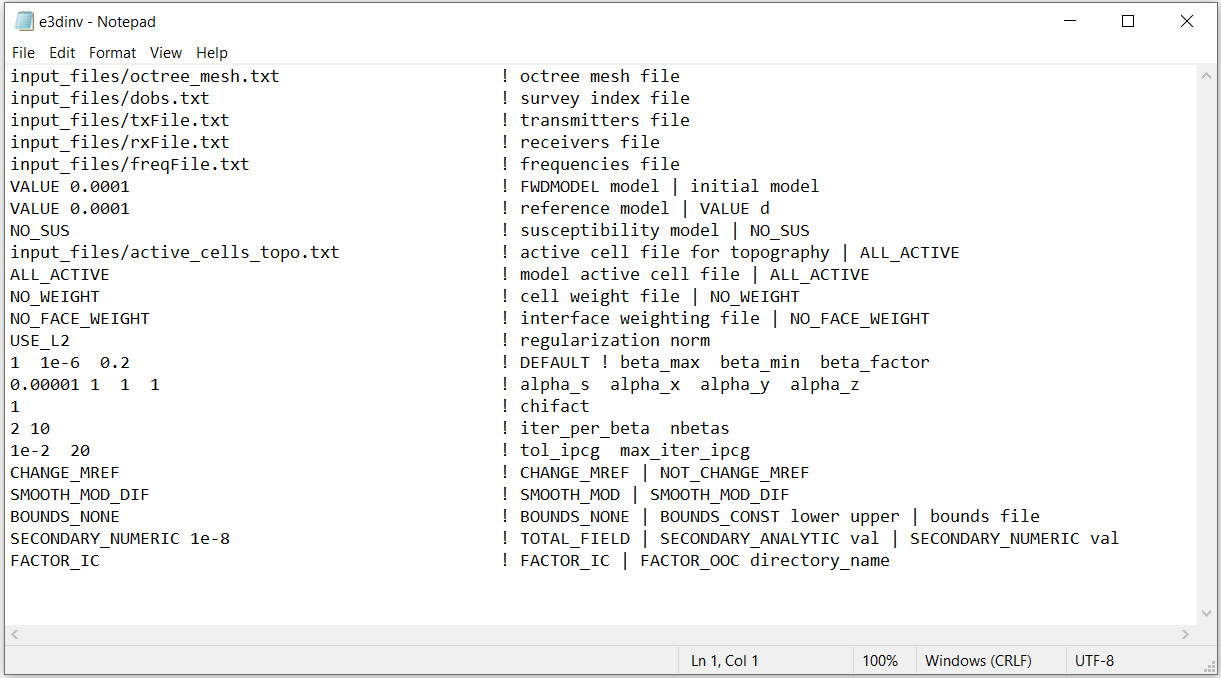
Fig. 3.5 Example input file for running the inversion (Download ). Example input file for forward modeling (Download ).

3.2.5.1. Line Descriptions

• Inversion Mesh: file path to the inversion (OcTree) mesh file

• Observation File: file path to the observed data file

• Transmitter File: file path to the transmitter file

• Receiver File: file path to the receiver file

• Frequencies File: file path to the frequencies file

• Initial/FWD Model: On this line we specify either the starting model for the inversion or the conductivity model for the forward modeling. On this line, there are 3 possible options:

  • If the program is being used to forward model data, the flag ‘FWDMODEL’ is entered followed by the path to the conductivity model.

  • If the program is being used to invert data, only the path to a conductivity model is required; e.g. inversion is assumed unless otherwise specified.

  • If a homogeneous conductivity value is being used as the starting model for an inversion, the user can enter “VALUE” followed by a space and a numerical value; example “VALUE 0.01”.

Important

If data are only being forward modeled, only the active topography cells and tol_ipcg max_iter_ipcg fields are relevant. However, the remaining fields must not be empty and must have correct syntax for the code to run.

• Reference Model: The user may supply the file path to a reference conductivity model. If a homogeneous conductivity value is being used for all active cells, the user can enter “VALUE” followed by a space and a numerical value; example “VALUE 0.01”.

• Susceptibility Model: The user may supply the file path to a background susceptibility model. If the Earth is non-susceptible, the user may enter a flag of NO_SUS.

• Active Topography Cells: Here, the user can choose to specify the cells which lie below the surface topography. To do this, the user may supply the file path to an active cells model file or type “ALL_ACTIVE”. The active cells model has values 1 for cells lying below the surface topography and values 0 for cells lying above.

• Active Model Cells: Here, the user can choose to specify the model cells which are active during the inversion. To do this, the user may supply the file path to an active cells model file or type “ALL_ACTIVE”. The active cells model has values 1 for cells lying below the surface topography and values 0 for cells lying above. Values for inactive cells are provided by the background conductivity model.

• Cell Weights: Here, the user specifies whether cell weights are supplied. If so, the user provides the file path to a cell weights file If no additional cell weights are supplied, the user enters “NO_WEIGHT”.

• Face Weights: Here, the user specifies whether face weights are supplied. If so, the user provides the file path to a face weights file cell weights file. If no additional cell weights are supplied, the user enters “NO_FACE_WEIGHT”. The user may also enter “EKBLOM” for 1-norm approximation to recover sharper edges.

• Sparseness: The sparseness of the recovered model is determined by the terms within the model objective function . A standard approach is to use an L2-norm for all terms

  • To use the L2-norm, enter the flag ‘USE_L2’

  • To specify the Ekblom norm, enter the flag ‘USE_EKBLOM’ followed by values for \(p\) and \(\varepsilon\) where the Ekblom norm is given by:

\[\sum_{i=1}^M \, (\sigma_i^2 + \varepsilon^2)^{p/2} \;\;\; \textrm{s.t.} \;\;\; 1\leq p \leq 2, \; \varepsilon > 0\]

• beta_max beta_min beta_factor: Here, the user specifies protocols for the trade-off parameter (beta). beta_max is the initial value of beta. beta_min is generally used to denote the minimum allowable trade-off parameter the program can use before quitting. For this code however, the minimum beta is determined through the nBeta parameter on line 15 and the beta_min parameter has no function. beta_factor defines the factor by which beta is decreased at each iteration; example “1E4 10 0.2”. The user may also enter “DEFAULT” if they wish to have beta calculated automatically. See theory on cooling schedule.

• alpha_s alpha_x alpha_y alpha_z: Alpha parameters . Here, the user specifies the relative weighting between the smallness and smoothness component penalties on the recovered models.

• Chi Factor: The chi factor defines the target misfit for the inversion. A chi factor of 1 means the target misfit is equal to the total number of data observations. For more, see the GIFtools cookbook .

• iter_per_beta nBetas: Here, iter_per_beta is the number of Gauss-Newton iterations per beta value. nBetas is the number of times the inverse problem is solved for smaller and smaller trade-off parameters until it quits. See theory section for cooling schedule and Gauss-Newton update.

• tol_ipcg max_iter_ipcg: Here, the user specifies solver parameters. tol_ipcg defines how well the iterative solver does when solving for \(\delta m\) and max_iter_ipcg is the maximum iterations of incomplete-preconditioned-conjugate gradient. See theory on Gauss-Newton solve

• Reference Model Update: Here, the user specifies whether the reference model is updated at each inversion step result. If so, enter “CHANGE_MREF”. If not, enter “NOT_CHANGE_MREF”.

• Hard Constraints: SMOOTH_MOD runs the inversion without implementing a reference model (essential \(m_{ref}=0\)). “SMOOTH_MOD_DIF” constrains the inversion in the smallness and smoothness terms using a reference model.

• Bounds: Bound constraints on the recovered model. Choose “BOUNDS_CONST” and enter the values of the minimum and maximum model conductivity; example “BOUNDS_CONST 1E-6 0.1”. Enter “BOUNDS_NONE” if the inversion is unbounded, or if there is no a-prior information about the subsurface model.

• Field Options: The user can model the total field or the secondary field. In the latter case, the user may choose whether the primary field is computed analytically or numerically for a homogeneous background conductivity.

  • Use the flag TOTAL_FIELD to model the total field.

  • Use the flag SECONDARY_ANALYTIC followed by a value for the background conductivity to model the secondary field. In this case, the code will compute the total field for the conductivity model provided, then subtract the analytic total field using the homogeneous background conductivity provided. To subtract the free-space primary field, let the background conductivity be 1e-8 S/m.

  • Use the flag SECONDARY_NUMERIC followed by a value for the background conductivity to model the secondary field. In this case, the code will compute the total field for the conductivity model provided, then subtract the numerically computed total field using the homogeneous background conductivity provided. To subtract the free-space primary field, let the background conductivity be 1e-8 S/m.

• Memory Options: This code uses a factorization to solve the forward system at each frequency. These factorizations must be stored. By using the flag ‘FACTOR_IC’ (in cpu), factorizations are stored within a computer’s RAM. Although this is faster, larger problems cannot be solved if insufficient temporary memory is available. The factorizations are stored in permanent memory (disk) if the flag ‘FACTOR_OOC’ (out of cpu) is used followed by the path to a directory. This is slower because the program must read these files many times. The second options is ill-advised if files are being transferred over a network.